Introduction

Generative art is a contemporary art form that employs algorithms, artificial intelligence, and computer programs to create artworks. In contrast to traditional art, where the artist works with form and color to independently create a piece, generative art is implemented through a defined set of rules and algorithms, leading to the automatic generation of images, sounds, animations, or texts. This art form often utilizes randomness, recursion, and feedback loops to create unique and unpredictable works.

At IT-Dimension, we have explored some of the common methods (randomness, feedback loops, recursion, cellular automata, L-systems, genetic algorithms, particle systems, noise functions like Perlin, fractals, Markov chains, Voronoi diagrams, Delaunay triangulation, chaos theory, and more) used in generative art and how they are employed in the creation of such works.

To generate images, we wrote scripts in Python using various libraries, as well as Processing scenarios in Java. They are executed from a specially developed C# application. It’s important to note that to achieve acceptable results, the scripts may need to be run multiple times, and the desired outcome should be saved as a graphical file.

Randomization, Pixels, and Shapes

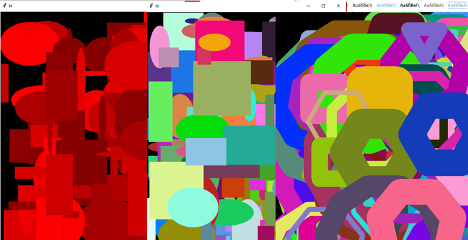
The simplest implementation of generative art images can be achieved through the use of randomization. In all script implementations, randomization is heavily utilized: object coordinates, colors, sizes, mathematical formulas, noise parameters, scaling factors, and more are chosen randomly. Additionally, pixel rendering is employed to create such images:

Greater effect can be achieved by varying the color palette in different image clusters and simple shapes:

From left to right: a monochrome image with shades of a randomly selected color, a full palette, and using of turtle graphics – the Turtle package in Python

It is also possible to create a multilayer structure:

Light pallette on the background

Pixeled layer on the background

Fractals

All fractal images share the following key characteristics:

• Self-similarity – fractals exhibit exact, approximate, or statistical self-similarity.
• Algorithmic nature – fractals are constructed using a simple recursive algorithm.
• Multidimensionality – details of fractals are evident at any observation scale.
• Non-uniformity – the fractal structure is too irregular to be described in terms of classical geometry.
• Repetition – the same patterns in fractals recur everywhere but with slight variations each time. We continually discover something new while still recognizing familiar outlines.
• Incompleteness – a fractal is never presented in clear finality; the visual representations of a fractal are always manifestations of incompleteness.

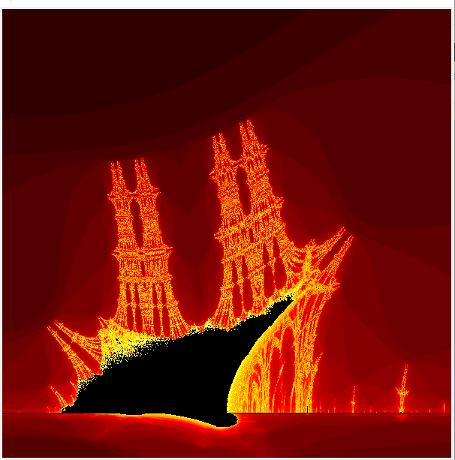
Mandelbrot Fractal

The Mandelbrot fractal is a set of points on the complex plane for which the iterative sequence (*) with an initial condition does not diverge to infinity.

Shown above Mandelbrot fractal in its classical form can be used to generate fractals of a similar nature. For instance, the script for the Fire fractal (like many other Mandelbrot’s ones), represents a fractal of escape-time nature using a system similar to the Mandelbrot equations. By altering the formulas and adjusting the user space, a diverse family of fractals can be obtained. Furthermore, it is possible to modify the color scheme (here, red, orange, and yellow are used).

Julia Set

Every point z on the complex plane exhibits its own behavior (either remaining finite, tending towards infinity, or assuming fixed values) during iterations of the function f(z), and the entire plane is divided into distinct parts.

In other words, the set of points on the complex plane, that do not diverge to infinity with increasing iterations of n, form Julia Set. Its implementation also allows for the creation of stunningly beautiful images.

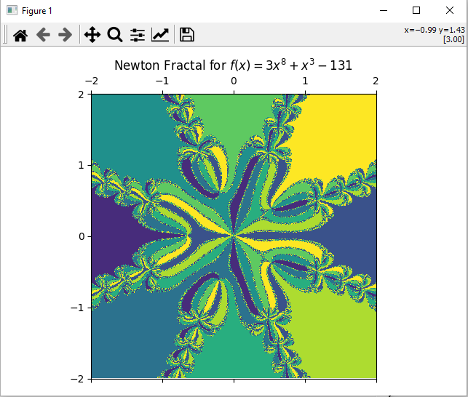
Newton Fractal

The Newton Fractal can be easily implemented using the FractPy library, which relies on Sympy, numpy, and matplotlib – all of which are part of the standard Python scientific stack, making it straightforward to install on all operating systems. It’s easy to use by calling functions for creating corresponding fractals, defined as polynomial functions by this library (currently, the library offers a limited set of functions for creating fractals). Different fractals can be obtained by modifying the polynomial function.

Newton Fractal example

This fractal is derived from the polynomial shown in the graph and, accordingly, divides the plane into 8 segments (according to the polynomial’s degree).

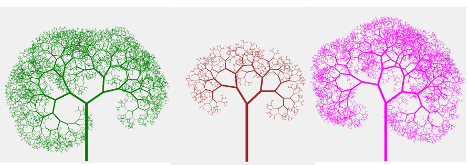
L-Systems, Fractal Trees

An L-system (or Lindenmayer system) is a parallel rewriting system and a type of formal grammar. In simpler terms, an L-system consists of an alphabet of symbols that can be used to create strings, a set of production rules that specify substitutions for each symbol, an initial string (“axiom”) to start the construction, and a mechanism for translating the resulting string into geometric structures. The most basic example of an L-system is the task of constructing a tree.

A script has been implemented to build such a fractal tree, which is based on a recursive branch generation function initiated after drawing the trunk. The recursive function’s exit condition is a branch length smaller than a specified value, which can be randomized. The angles of branch inclinations can also be randomized, with all these random values selected within a defined range in interactive mode. As a result, we can generate a collection of fractal trees.

Forest (grove), created by iterating the generated code and shifting the position of the trunk:

Noise Functions (Processing)

From a formal and technical perspective, Processing is a C-like programming language based on Java (a modified version of Java with drawing primitives) which was created in 2001. Programs in the Processing language are represented as small text files and are called “sketches.” The sketch template includes two functions: void setup() {} void draw() {}

In the setup() function, we define the initial parameters for our sketch, such as image size, background color, color palette, and more. The draw() function serves as the main (infinite) program loop in which we perform all the necessary actions, including dynamic image generation.

In the Processing language, there is a function called noise(). It produces values between 0 and 1 (centered around 0.5) for certain input data. These values are random, but they repeat when the input data and seed values are repeated. Another property of this function is that the noise is continuous: similar input data yield nearly identical values. Calculating noise values is fast, and there’s no need to calculate previous values. This function in Processing is called Perlin noise, returning Perlin noise at specified coordinates. Perlin noise is a generator of a random sequence that produces a more natural, harmonious sequence of numbers compared to the standard random function.

With different algorithms we get different scenarios:

Scenarios are executed dynamically, but there is the option to obtain a set of frames for a specified number of frame images, from which an animated GIF can be generated, or a specific GIF frame can be selected.

Other Methods of Image Generation

Procedural generation of random abstract images can be achieved by constructing a random mathematical function that takes coordinates x, y, coordinates the colors, and evaluates them for each pixel.

The algorithm builds a random mathematical formula in the form of a parse tree, working recursively from top to bottom. Each node is randomly selected and has a constant color, one of the variables x or y, or a function. Functions here utilize sin and cos (from the numpy library) as well as the four basic arithmetic operators +, -, *, and /. Of course, we can choose any set of functions, which will alter the nature of the generated images.

After selecting a function, all required arguments are recursively generated, and then the function is evaluated. Here’s an example of an image generated in this manner:

Interesting images can be obtained using the Python PIL (Pillow) library. The Image.merge() function in the Pillow module combines a set of single-channel (monochromatic) images into a new multi-channel image: Image.merge(“RGB”, (red_image, green_image, blue_image)).

Do not forget that to achieve the desired (acceptable) effect, scripts must be run many times due to the extensive randomization of many parameters.

Artificial Intelligence in Generative Art

The application of artificial intelligence and machine learning in generative art is a significant aspect that cannot be overlooked. Artificial intelligence (AI) can be utilized in generative art in two ways. The first approach involves harnessing the capabilities of AI to realize a human’s creative idea. The second approach is to train artificial intelligence on paintings and treat it as a co-author. Perhaps the simplest example of the first approach is cognitive portraiture. In this method, photos of individuals are overlaid on top of one another automatically in such a way that specific facial features align. By using anchor points on the face (typically achieved using the dlib library with 68 points), an averaged portrait can be obtained.

A neural network operates somewhat like our brain. It consists of artificial neurons that sum signals from their inputs and transmit them to the output. At the next level, the signals from previous layers of neurons are again summed and passed to the output. The desired result is achieved in the end.

Here’s an example of what a neural network might consider to be good pictures, although a person might only consider the image on the right to be a good landscape:

Hence, to achieve any interesting outcome, human participation is indispensable. Similarly, as discussed in the aspects above, the images exhibit a wide diversity with each run of the scripts and sketches, and each individual will also select what appeals to them.

Conclusion

It’s evident that with the continuous advancement of technology, especially in the realm of artificial intelligence and machine learning, generative art will continue to evolve and unveil new possibilities for artists and designers. Perhaps in the future, generative methods will be employed to create even more complex and dynamic works that can adapt and respond to changes in the environment and socio-cultural context, giving rise to more intricately composed projects.

Generative art is an undeniable phenomenon that continues to transform art and culture. It opens new horizons for creativity, interaction, and learning while posing intriguing questions about the nature of authorship and originality in the modern world. Generative art will persist in its development and contribute to the diversity of the cultural landscape. The aspects of generative art discussed above, including methodologies, techniques, and algorithms, can undoubtedly be in demand in various contexts, depending on specific needs.

The illustrative material presented in this article is generated based on implemented software: Python scripts run from a C# application (they can also be run autonomously), and sketches written in the Processing language (Java).

In conclusion, we should answer the question: what was the initial purpose of creating the software for generative art? And here it’s worth noting, that generative art has long become a part of our daily lives, finding extensive application in video art, print media, web design, architecture, interior design, fashion design, furniture, and more, giving rise to a unique aesthetics.

At IT-Dimension, we think that now everyone has the opportunity to feel like an artist or musician, creating musical patterns to suit their mood or crafting a unique painting using various software, including one that was used in the creation of this article. Generative art seems to be one of the most intriguing and promising directions in the realm of art, progressing by leaps and bounds.